數位家庭(DigiFamily)

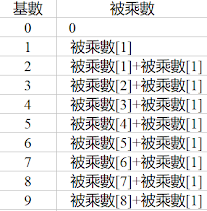
 以滾動式進位計算大數乘法 計算 (n位被乘數) X (m位乘數)，以傳統方式計算乘法，我們通常需要 n X m 次乘法及 2n(m-1) 次加法，更甚者，運算過程中是乘法與加法混合在一起，而這也是手算不易及造成錯誤的根源，若將計算思路稍微改變一下，不僅可減少計算時間，也能提高計算結果的正確性，這也是本文提出滾動式進位演算法(Rolling Carry Algorithm)的初衷。 我們知道乘法可以改成加法計算，以 3 X 2 = 6 來說，一般人會直覺的就是把 3 加 2 次或 2 加 3 次，但若是 33 X 22 或 333 X 222 抑或是更大的數字呢！那原本簡單的思維大概無法處理了，誰也無法忍受把 333 加 222 次罷。 雖說方法不好，但並不代表觀念錯誤，只需稍微改變一下思路，仍是大有可為的，滾動式進位演算法就是藉著改變計算方法，得到不僅手算及以電腦運算皆較佳的乘法計算方式，接著我們就來說說滾動式進位演算法的觀念， 首先，我們將被乘數當作一個完整的數字，並建立一個被乘數基數表，如下表， 接著，從被乘數基數表找到乘數相對應值，並循乘數的 LSD 至 MSD 逐次與前一進位相加，相加後保留個位數與前一運算以文字相加，其餘皆是次一進位，完成所有乘數運算即得到運算之積。 範例  12170126 X 258 = ? 大數乘法程式流程圖範例 大數乘法 Python 程式範例

 如何於 VS Code 內啟動 Python 的虛擬環境 01.啟動 VS Code 02.於 VS Code 的檔案總管開啟 Python 資料夾，此時於 VS Code 終端機可看到如  ps c:\0My\Pythons\SpaceShip 的回覆字元，這表示目前終端機處於系統的終端機模式(PowerShell)。 03.以 cmd 指令將系統切換為 命令提示字元 模式，系統的回覆字元將會變為c:\0My\Pythons\SpaceShip。 04.以 python -m venv .venv 指令建立虛擬環境，此時開啟的資料夾會多出一個 .venv 資料夾。 05.以 .venv\Scripts\activate.bat  指令啟動 Python 的虛擬環境，此時可看到(.venv)c:\0My\Pythons\SpaceShip 的系統回覆字元。 06.以 .venv\Scripts\deactivate.bat 關閉 Python 的虛擬環境。 07.以 pip list 指令查看已安裝套件。 08.安裝套件範例 pip install pygame